Difference between revisions of "Dev:Bone Layer"
(→What happen if there are more than one bone affecting the point?) |
m (moved Bone Layer to Dev:Bone Layer) |
||
| (43 intermediate revisions by 4 users not shown) | |||
| Line 6: | Line 6: | ||
== Concepts == | == Concepts == | ||
| − | This is | + | This is an unsorted list of concepts to let me clarify my thoughts and also allow others to understand the following sections. |
=== Bones intentions === | === Bones intentions === | ||
| − | Initial intention of Bones is attempt to emulate the skeleton of a vertebrate animal. In this way you have | + | Initial intention of Bones is to attempt to emulate the skeleton of a vertebrate animal. In this way you have the skin and a skeleton. Part of the skin are associated with the various bones of the skeleton. When the skeleton moves the skin follows. |
=== Application of bones in animation === | === Application of bones in animation === | ||
| − | In traditional animation | + | In traditional animation producing a walk cycle implies drawing each keyframe for the walk and maybe, depending on the walking speed, drawing the in betweens too. To avoid having to draw the in between images there are tweening animation programs (like Synfig) to help the animator. Then the animator just needs to draw the keyframes and the application does the rest. That's quite good but in certain situations you see your self redrawing the same pose (with small variations) frequently at different times. Then bones come to help. They aid the animator in the following manner. |
* With the manipulation of a single object (or a set of them) you can manage a lot of points of the drawing definition. | * With the manipulation of a single object (or a set of them) you can manage a lot of points of the drawing definition. | ||
| − | * Rotations of drawings using keyframes needs lots of them (by | + | * Rotations of drawings using keyframes needs lots of them (by nature of the fact that tweening is defined in the x,y coordinates system and the rotation is performed in the angle, radius coordinate system). Using bones you can perform rotations of large angles with just two waypoints. Also since characters have limbs and limbs in living beings do mainly rotations, the usage of bones becomes handy in that kind of animation. |
| − | * Once the character (or whatever thing that uses bones) is rigged (the skeleton structure is created and the relationship between the skin | + | * Once the character (or whatever thing that uses bones) is rigged (the skeleton structure is created and the relationship between it and the skin is defined) it is possible to produce different kinds of keyframes for different purposes: Walk, run, jump, sit, ... |
| − | == How can we do this | + | == How can we do implement this? == |
| − | + | The relationship between the skeleton and the skin is like this: | |
| − | The relationship between the skeleton and the skin is | + | |
| − | The Skin is made | + | *The Skin is made using Points and BLines. BLines are defined by Points. Points are made of Vertexes and Tangents |
| + | *Skeleton is made of bones and the relationships between them. | ||
| + | *''If Bones would have influence on the Vertexes and Tangents then the bones movements would move the points and therefore the skin would be moved''. | ||
| − | + | That's the key, if we understand how a bone has influence on a vertex and a tangent then we can find the way a skeleton can have influence over a skin. | |
| − | + | === Bones Properties === | |
| + | From my experience with bones in other 2D animation applications, watching the strong and weak points, bones needs to have the following properties: | ||
| − | + | * A bone has an origin point about which the rotation is performed. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | * A bone has | + | |
* A bone has a length. | * A bone has a length. | ||
| − | * A bone has an angle | + | * A bone has an angle. |
| − | * A bone | + | * A bone can have a region of influence. |
| − | * A bone can have a | + | * A bone can have a one or zero parent bones. |
| − | * A bone can have one | + | * A bone can have one or more child bones. |
| + | * A skeleton is defined as a connected set of bones (consisting of exactly one parent-less bone and its children bones and their descendants). | ||
| − | All the bones | + | All the bones in a Synfig Document can produce several distinct skeletons (depending on how many parent-less bones are in it). |
=== How does a Vertex move under the influence of a single Bone? === | === How does a Vertex move under the influence of a single Bone? === | ||
| − | Conceptually a bone has influence over a point doing [http://en.wikipedia.org/wiki/Affine_transformation affine | + | Conceptually a bone has influence over a point by doing [http://en.wikipedia.org/wiki/Affine_transformation affine transformations] of its position according to the bone values. See also [http://en.wikipedia.org/wiki/Transformation_matrix transformation matrix]. A bone produces rotation, scale and translation to a point in this way: |
| − | + | {{l|Image:Bonesimulation2.png}} | |
| − | As you can see the values that | + | As you can see the values that produce the movement of the point P to the point P' are given by: |
*Translation of the bone: O'-O | *Translation of the bone: O'-O | ||
| − | *Rotation of the bone: alpha'-alpha | + | *Rotation of the bone: <math>\alpha'-\alpha</math> |
*Scale of the bone: s=length'/length | *Scale of the bone: s=length'/length | ||
| − | Then, given a Point P in the 2D space and | + | Then, given a Point P in the 2D space and knowing the translation, rotation and scale of the bone you can calculate the new position P' using this formula: |
<math> | <math> | ||
| Line 65: | Line 63: | ||
<math> | <math> | ||
| − | R(-alpha)=\begin{bmatrix} | + | R(-\alpha)=\begin{bmatrix} |
| − | \cos(-alpha) & \sin(-alpha) & 0 \\ | + | \cos(-\alpha) & \sin(-\alpha) & 0 \\ |
| − | -\sin(-alpha) & \cos(-alpha) & 0 \\ | + | -\sin(-\alpha) & \cos(-\alpha) & 0 \\ |
0 & 0 & 1 | 0 & 0 & 1 | ||
\end{bmatrix} | \end{bmatrix} | ||
| − | </math> Rotate an angle of amount '-alpha' | + | </math> Rotate by an angle of amount '<math>-\alpha</math>' about the origin. That aligns the bone with the X axis |
<math> | <math> | ||
| − | + | S_x(length'/length)=\begin{bmatrix} | |
length'/length & 0 & 0 \\ | length'/length & 0 & 0 \\ | ||
0 & 1 & 0 \\ | 0 & 1 & 0 \\ | ||
0 & 0 & 1 | 0 & 0 & 1 | ||
\end{bmatrix} | \end{bmatrix} | ||
| − | </math> Scale a value of 's=length'/length' in the direction of X (the current direction of the bone). | + | </math> Scale by a value of 's=length'/length' in the direction of X (the current direction of the bone). |
<math> | <math> | ||
| − | R(alpha)=\begin{bmatrix} | + | R(\alpha^')=\begin{bmatrix} |
| − | \cos(alpha^') & \sin(alpha^') & 0 \\ | + | \cos(\alpha^') & \sin(\alpha^') & 0 \\ |
| − | -\sin(alpha^') & \cos(alpha^') & 0 \\ | + | -\sin(\alpha^') & \cos(\alpha^') & 0 \\ |
0 & 0 & 1 | 0 & 0 & 1 | ||
\end{bmatrix} | \end{bmatrix} | ||
| − | </math> Rotate an angle of amount 'alpha'' | + | </math> Rotate by an angle of amount '<math>\alpha'</math>' about the origin. |
<math> | <math> | ||
| − | + | T(O^')=\begin{bmatrix} | |
1 & 0 & 0 \\ | 1 & 0 & 0 \\ | ||
0 & 1 & 0 \\ | 0 & 1 & 0 \\ | ||
| Line 96: | Line 94: | ||
</math> Translation to new position O' | </math> Translation to new position O' | ||
| − | Then the transformation from P to P' is | + | Then the transformation from P to P' is given by the matrix multiplication: |
| − | <math> P'=P\cdot T(-O)\cdot R(-alpha) S_x(length'/ | + | <math> P'=P\cdot T(-O)\cdot R(-\alpha)\cdot S_x(length'/length)\cdot R(\alpha^')\cdot T(O^')</math> |
| + | |||
| + | <math> P'=P\cdot T\cdot R\cdot S_x\cdot R'\cdot T'=P\cdot B</math> | ||
| + | |||
| + | === Can Points (Bone influenced) be moved independently? === | ||
| + | |||
| + | Yes, they should be. If not the animator is restricted to only doing the animation with bones which would lead to some insoluble problems during the animation. Considering this, the point position result comes from the addition of two terms: | ||
| + | *(a) The movement of the point as described by the influence of the bone(s): P(B) | ||
| + | *(b) The free movement of the point in the 2D space. P(animated) | ||
| + | |||
| + | In terms of the interface with the user, the value P(animated) is just obtained in this way: | ||
| + | |||
| + | #In any position of the time line (bones are animated) the point has a position given by the influence of the bones: P(B). | ||
| + | #The user selects a point, drags it, placing it at P'. | ||
| + | #The final position of the point is P' but the user cannot modify the first term P(B) so the second term (b) becomes: P(animated)=P'-P(B). | ||
===What happen if there are more than one bone affecting the point?=== | ===What happen if there are more than one bone affecting the point?=== | ||
| − | The first thing you can think when you deal with more than one bone | + | The first thing you can think when you deal with more than one bone having influence over the same point is to calculate the average of the sum of the influences of all bones. So if there are N bones affecting the point then we can think of summing all the resulting points from each bone and then dividing the result by N to not scale the result. |
<math> B=\frac{\sum_{k=1}^N B_k}{N} </math> | <math> B=\frac{\sum_{k=1}^N B_k}{N} </math> | ||
| Line 108: | Line 120: | ||
Where <math>B_k</math> is the bone matrix for the bone ''k'' on the point P. | Where <math>B_k</math> is the bone matrix for the bone ''k'' on the point P. | ||
| − | That's fine but I would like to have more control to the way the bones | + | That's fine but I would like to have more control to the way the bones affect the points. When you move a bone it looks reasonable that not all the points are influenced in the same way. This can be solved by using a "weighted" average instead of a plain one. That means giving a different amount of influence to one bone than to the other. |
<math> B=\frac{\sum_{k=1}^N B_k \cdot w_k}{\sum_{k=1}^N w_k} </math> | <math> B=\frac{\sum_{k=1}^N B_k \cdot w_k}{\sum_{k=1}^N w_k} </math> | ||
| Line 114: | Line 126: | ||
Where <math>w_k</math> is the weight for the bone ''k'' over the point P. | Where <math>w_k</math> is the weight for the bone ''k'' over the point P. | ||
| − | + | === Skeleton === | |
| + | |||
| + | A skeleton is a set of bones linked one to others in a tree hierarchy. A bone can have several children (or none) but only one parent (or none). This configuration allows to do a easy calculation of the forward kinematic (FK )of the chain and the inverse kinematic (IK) of the chain of bones. If the hierarchy were not tree type then the FK and IK can be not soluble. | ||
| + | |||
| + | For those IK and FK calculations it is good to have the bone referenced to its parent. So the parameters of the bone are described as relative to the parent bone. The parent bone defines a local coordinate system where the origin of the coordinate system lies on the Origin of the bone and the tip of the bone is pointing to the positive direction of the X axis. | ||
| + | |||
| + | {{l|Image: skeleton.png}} | ||
| + | |||
| + | As you can see in this image, each skeleton position and orientation is defined by the relative position of its immediate parent bone. In the diagram bone3 is a child of bone2 and bone 2 is a child of bone1. The bone 1 is the root parent bone but you can imagine it attached to a "master root bone" (defined by the origin of coordinates -red circumference- and the horizontal) so it can be said that the bone1 has its origin and angle defined relative to its "parent". | ||
| + | |||
| + | In this skeleton the three bones are parented in a linear way. But as you can imagine, following the rules stated for child-parent, a bone can have more than one child but not more than one parent. | ||
| + | That means that defined a bone in the skeleton, there is only one sequence of parents to reach the root parent of the skeleton. Also it means too that one root bone defines one skeleton so each skeleton has only one root bone and only one. | ||
| + | |||
| + | Consider this: B3 is child of B2 and B2 is child of B1. Also B4 is child of B2 and B5 is child of B4. The way to travel from B5 to B1 is unique: B5->B4->B2->B1. | ||
| + | |||
| + | === Setup and Animation === | ||
| + | |||
| + | During the animation of the skeleton it is supposed that the position of each bone, its angle and its scale changes. Position and angle are relative to the parent bone, but scale is a value that calculates the current length of the bone compared with the "original" bone length (scale=length'/length) as you can see from the original formulas in the previous section. That means that the "original" bone length shouldn't be never zero, otherwise there will be a division by zero and the scale of the bone becomes infinite. | ||
| + | |||
| + | Also, the final position P' of a point that moves influenced by a single bone is given by the original point position relative to the bone in its "original" position (P). | ||
| + | |||
| + | What I'm trying to explain is that it is needed that the setup of the bone (position, alpha and length) and the setup position of the point (P) to be moved would be given to calculate the final position of the point (P') given a moved position of the bone (position', alpha', length') | ||
| + | |||
| + | Said this and considered the information of the previous sections, the bones and points that are influenced from the bones should have the following parameters: | ||
| + | |||
| + | '''BONES PARAMETERS''' | ||
| + | {| | ||
| + | ! Parameter !! Notation !! Type !! Animated !! Comment | ||
| + | |- | ||
| + | | Origin ||<math> \textstyle O_j(t) </math> || Vector (Real,Real) ||Yes|| Relative to the parent | ||
| + | |- | ||
| + | | Angle || <math> \textstyle \alpha_j(t) </math> || Angle (DEG) ||Yes|| Relative to the parent | ||
| + | |- | ||
| + | | Length || <math> \textstyle l_j(t) </math> || Real ||Yes|| Calculated, not animatable. | ||
| + | |- | ||
| + | | Scale || <math> \textstyle s_j(t) </math> || Real ||Yes|| <math> \textstyle l_j(t) =l^0_j \cdot s_j(t) </math> | ||
| + | |- | ||
| + | | Setup Origin || <math> \textstyle O^0_j(t) </math> || Vector (Real,Real) ||Yes|| Relative to the parent | ||
| + | |- | ||
| + | | Setup Angle || <math> \textstyle \alpha^0_j(t) </math> || Angle (DEG) ||Yes|| Relative to the parent | ||
| + | |- | ||
| + | | Setup Length || <math> \textstyle l^0_j </math> || Real || No|| Constant, zero not allowed. | ||
| + | |- | ||
| + | | Setup Scale || <math> \textstyle s^0_j </math> || Real || No|| <math> \textstyle s^0_j = 1 </math> | ||
| + | |- | ||
| + | | Parent || <math> \textstyle PBone_j(t) </math> || Bone ||Yes|| | ||
| + | |} | ||
| + | |||
| + | |||
| + | '''POINT PARAMETERS''' | ||
| + | |||
| + | {| | ||
| + | ! Parameter !! Notation !! Type !! Animated !! Comment | ||
| + | |- | ||
| + | | Position ||<math> \textstyle V(t) </math> || Vector (Real,Real) ||Yes|| Calculated: <math> \textstyle V(t) =VF(t) + VS(t) \cdot M(t) </math> Global coordinates | ||
| + | |- | ||
| + | | Free Position ||<math> \textstyle VF(t) </math> || Vector (Real, Real) ||Yes|| Global Coordinates | ||
| + | |- | ||
| + | | Setup Position ||<math> \textstyle VS(t) </math> || Vector (Real, Real) ||Yes|| Global Coordinates | ||
| + | |- | ||
| + | | Bone Influence Matrix ||<math> \textstyle M(t) </math> || Matrix (3x3) ||Yes|| Calculated. See formulas below | ||
| + | |- | ||
| + | | Bone Influence Id ||<math> \textstyle BoneID_i </math> || Bone || No || 'i' is the index for all the Bones that influences on the Point | ||
| + | |- | ||
| + | | Influence weight ||<math> \textstyle w_i </math> || Real || Yes || the weight associated to the BoneID_i | ||
| + | |} | ||
| + | |||
| + | (t) denotes ''calculated at the time t'' | ||
| + | |||
| + | === Position of a Point due to Bones Influence === | ||
| + | |||
| + | According to the table, the final position of a point influenced by the bones is calculated based on two terms: A free movement of the point plus a bone drive movement. In this section we are going to calculate the second term. | ||
| + | |||
| + | <math> \textstyle V(t) =VF(t) + VS(t) \cdot M(t) </math> | ||
| + | |||
| + | <math> M(t) = \cfrac{\sum_{i=1}^N M_i(t) \cdot w_i(t)}{\sum_{i=1}^N w_i(t)} </math> | ||
| + | |||
| + | <math> M_i(t)=B^0_i(t) \cdot B_i(t) </math> | ||
| + | |||
| + | where i is a index that runs all the Bones Influence ID from i=1 to N (N= total number of bones that influence to the point) | ||
| + | |||
| + | <math> B^0_i(t)= \prod_{j=root}^{j=i} C_j^0(t)</math> | ||
| + | |||
| + | <math> B_i(t)= \prod_{j=i}^{j=root} C_j(t)</math> | ||
| + | |||
| + | where 'j' runs the bone skeleton jumping from a child/parent bone to a parent/child bone each time. The travel of the index 'j' from ''root'' to ''i'' and from ''i'' to ''root'' is fixed -and unique- by the nature of skeletons constructions (a bone, a parent), as mentioned before. | ||
| + | |||
| + | <math> C_j^0(t) = T(-O_j^0(t)) \cdot R(-\alpha_j^0(t)) \cdot S_x(\frac{1}{s^0_j})</math> | ||
| + | |||
| + | This matrix calculates the position of the point in local coordinates in relation to the bone 'j' at setup position. Notice that <math> s^0_j </math> is equal to <math> \textstyle 1 </math> for any bone and for any time. | ||
| + | |||
| + | <math> C_j(t) = S_x(s_j(t))\cdot R(\alpha_j(t)) \cdot T(O_j(t)) </math> | ||
| + | |||
| + | This matrix calculates the global position of the point due to the bone 'j' at animated position of the skeleton. | ||
| + | |||
| + | === Calculate the position and angle of a bone in a skeleton === | ||
| + | |||
| + | |||
| + | ==== Position and Angle at Setup ==== | ||
| + | |||
| + | If the bones are described using relative coordinates to its predecessor, the position <math>\textstyle Q^0_j</math> and the angle <math>\textstyle \beta^0_j</math> of the bone 'j' in relation to the "master root bone" (ie. the global coordinate system) is given by those equations: | ||
| + | |||
| + | <math>Q^0_j(t) = O^0_j(t) \cdot B^0_j(t)</math> | ||
| + | |||
| + | <math>\beta^0_j(t) = \sum_{i=root}^{j} \alpha^0_i(t)</math> | ||
| + | |||
| + | where | ||
| − | + | <math>B^0_j(t)=\prod_{i=root}^{parent} B^0_i(t)</math> | |
| − | + | where 'i' goes form the root bone to the parent of the bone 'j' and climbs down by one child each time until it reaches the 'parent of bone j' bone of the skeleton. | |
| − | + | <math>B^0_i(t)= T(-O^0_i(t)) \cdot R(-\alpha^0_i(t)) \cdot S_x(\frac{1}{s^0_j})</math> | |
| − | + | <math>B^0_i(t)</math> is the inverse matrix transformation of the position of the bone relative to its immediate parent. | |
| − | <math> | + | Notice that at setup, <math>s^0_j</math> is always equal to 1. |
| − | + | ====Animated Position and Angle ==== | |
| − | + | Once calculated the position and angle of a bone in global coordinates you can calculate its animated position and angle by the transformation of their parents in the skeleton. | |
| − | + | <math>Q_j(t) = O^0_j(t) \cdot B^0_j(t) \cdot B_j(t)</math> | |
| − | + | <math>\beta_j(t)= \beta^0_j(t) + \sum_{i=parent}^{root} \alpha_i(t)</math> | |
| − | <math> | + | where <math>B_j(t)=\prod_{i=parent}^{root} B_i(t)</math> |
| − | + | where 'i' goes form the parent bone and jumps up by one parent each time until it reaches the 'root' bone of the bone 'j'. | |
| − | + | <math>B_i(t)= S_x(s_j(t)) \cdot R(\alpha_i(t)) \cdot T(O_i(t)) </math> | |
| − | <math> | + | <math>\textstyle B_i(t)</math> is the transformation matrix of the position of the bone 'j' at the time t. |
| − | + | The results <math>\textstyle Q_j(t), \beta_j(t)</math> are obtained in global coordinates. | |
Latest revision as of 09:04, 19 February 2010
Contents
- 1 Initial seed for concepts
- 2 Concepts
- 3 How can we do implement this?
- 3.1 Bones Properties
- 3.2 How does a Vertex move under the influence of a single Bone?
- 3.3 Can Points (Bone influenced) be moved independently?
- 3.4 What happen if there are more than one bone affecting the point?
- 3.5 Skeleton
- 3.6 Setup and Animation
- 3.7 Position of a Point due to Bones Influence
- 3.8 Calculate the position and angle of a bone in a skeleton
Initial seed for concepts
This portion of IRC logs sets the basis for the implementation of a Bone Layer. The interesting part is from 16:49 to 18:56.
Also this one has some interesting thoughts. From 8:20 to 14:43
Concepts
This is an unsorted list of concepts to let me clarify my thoughts and also allow others to understand the following sections.
Bones intentions
Initial intention of Bones is to attempt to emulate the skeleton of a vertebrate animal. In this way you have the skin and a skeleton. Part of the skin are associated with the various bones of the skeleton. When the skeleton moves the skin follows.
Application of bones in animation
In traditional animation producing a walk cycle implies drawing each keyframe for the walk and maybe, depending on the walking speed, drawing the in betweens too. To avoid having to draw the in between images there are tweening animation programs (like Synfig) to help the animator. Then the animator just needs to draw the keyframes and the application does the rest. That's quite good but in certain situations you see your self redrawing the same pose (with small variations) frequently at different times. Then bones come to help. They aid the animator in the following manner.
- With the manipulation of a single object (or a set of them) you can manage a lot of points of the drawing definition.
- Rotations of drawings using keyframes needs lots of them (by nature of the fact that tweening is defined in the x,y coordinates system and the rotation is performed in the angle, radius coordinate system). Using bones you can perform rotations of large angles with just two waypoints. Also since characters have limbs and limbs in living beings do mainly rotations, the usage of bones becomes handy in that kind of animation.
- Once the character (or whatever thing that uses bones) is rigged (the skeleton structure is created and the relationship between it and the skin is defined) it is possible to produce different kinds of keyframes for different purposes: Walk, run, jump, sit, ...
How can we do implement this?
The relationship between the skeleton and the skin is like this:
- The Skin is made using Points and BLines. BLines are defined by Points. Points are made of Vertexes and Tangents
- Skeleton is made of bones and the relationships between them.
- If Bones would have influence on the Vertexes and Tangents then the bones movements would move the points and therefore the skin would be moved.
That's the key, if we understand how a bone has influence on a vertex and a tangent then we can find the way a skeleton can have influence over a skin.
Bones Properties
From my experience with bones in other 2D animation applications, watching the strong and weak points, bones needs to have the following properties:
- A bone has an origin point about which the rotation is performed.
- A bone has a length.
- A bone has an angle.
- A bone can have a region of influence.
- A bone can have a one or zero parent bones.
- A bone can have one or more child bones.
- A skeleton is defined as a connected set of bones (consisting of exactly one parent-less bone and its children bones and their descendants).
All the bones in a Synfig Document can produce several distinct skeletons (depending on how many parent-less bones are in it).
How does a Vertex move under the influence of a single Bone?
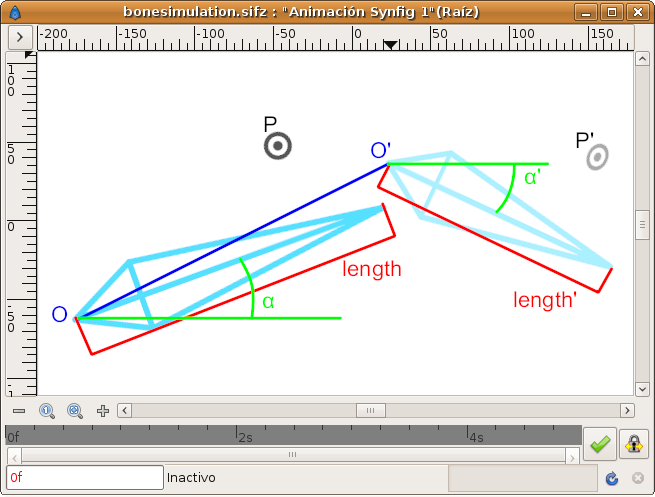
Conceptually a bone has influence over a point by doing affine transformations of its position according to the bone values. See also transformation matrix. A bone produces rotation, scale and translation to a point in this way:
As you can see the values that produce the movement of the point P to the point P' are given by:
- Translation of the bone: O'-O
- Rotation of the bone: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \alpha'-\alpha}
- Scale of the bone: s=length'/length
Then, given a Point P in the 2D space and knowing the translation, rotation and scale of the bone you can calculate the new position P' using this formula:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle T(-O)=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -O_x & -O_y & 1 \end{bmatrix} } Translation to origin (0,0)
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle R(-\alpha)=\begin{bmatrix} \cos(-\alpha) & \sin(-\alpha) & 0 \\ -\sin(-\alpha) & \cos(-\alpha) & 0 \\ 0 & 0 & 1 \end{bmatrix} } Rotate by an angle of amount 'Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle -\alpha} ' about the origin. That aligns the bone with the X axis
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle S_x(length'/length)=\begin{bmatrix} length'/length & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} } Scale by a value of 's=length'/length' in the direction of X (the current direction of the bone).
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle R(\alpha^')=\begin{bmatrix} \cos(\alpha^') & \sin(\alpha^') & 0 \\ -\sin(\alpha^') & \cos(\alpha^') & 0 \\ 0 & 0 & 1 \end{bmatrix} } Rotate by an angle of amount 'Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \alpha'} ' about the origin.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle T(O^')=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ O^'_x & O^'_y & 1 \end{bmatrix} } Translation to new position O'
Then the transformation from P to P' is given by the matrix multiplication:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle P'=P\cdot T(-O)\cdot R(-\alpha)\cdot S_x(length'/length)\cdot R(\alpha^')\cdot T(O^')}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle P'=P\cdot T\cdot R\cdot S_x\cdot R'\cdot T'=P\cdot B}
Can Points (Bone influenced) be moved independently?
Yes, they should be. If not the animator is restricted to only doing the animation with bones which would lead to some insoluble problems during the animation. Considering this, the point position result comes from the addition of two terms:
- (a) The movement of the point as described by the influence of the bone(s): P(B)
- (b) The free movement of the point in the 2D space. P(animated)
In terms of the interface with the user, the value P(animated) is just obtained in this way:
- In any position of the time line (bones are animated) the point has a position given by the influence of the bones: P(B).
- The user selects a point, drags it, placing it at P'.
- The final position of the point is P' but the user cannot modify the first term P(B) so the second term (b) becomes: P(animated)=P'-P(B).
What happen if there are more than one bone affecting the point?
The first thing you can think when you deal with more than one bone having influence over the same point is to calculate the average of the sum of the influences of all bones. So if there are N bones affecting the point then we can think of summing all the resulting points from each bone and then dividing the result by N to not scale the result.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle B=\frac{\sum_{k=1}^N B_k}{N} }
Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle B_k} is the bone matrix for the bone k on the point P.
That's fine but I would like to have more control to the way the bones affect the points. When you move a bone it looks reasonable that not all the points are influenced in the same way. This can be solved by using a "weighted" average instead of a plain one. That means giving a different amount of influence to one bone than to the other.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle B=\frac{\sum_{k=1}^N B_k \cdot w_k}{\sum_{k=1}^N w_k} }
Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle w_k} is the weight for the bone k over the point P.
Skeleton
A skeleton is a set of bones linked one to others in a tree hierarchy. A bone can have several children (or none) but only one parent (or none). This configuration allows to do a easy calculation of the forward kinematic (FK )of the chain and the inverse kinematic (IK) of the chain of bones. If the hierarchy were not tree type then the FK and IK can be not soluble.
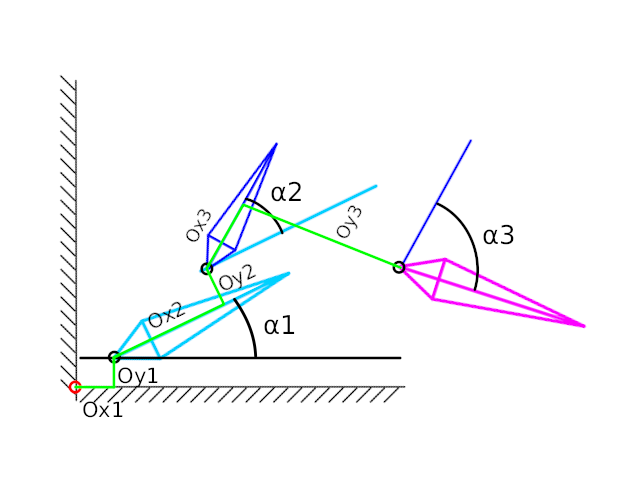
For those IK and FK calculations it is good to have the bone referenced to its parent. So the parameters of the bone are described as relative to the parent bone. The parent bone defines a local coordinate system where the origin of the coordinate system lies on the Origin of the bone and the tip of the bone is pointing to the positive direction of the X axis.
As you can see in this image, each skeleton position and orientation is defined by the relative position of its immediate parent bone. In the diagram bone3 is a child of bone2 and bone 2 is a child of bone1. The bone 1 is the root parent bone but you can imagine it attached to a "master root bone" (defined by the origin of coordinates -red circumference- and the horizontal) so it can be said that the bone1 has its origin and angle defined relative to its "parent".
In this skeleton the three bones are parented in a linear way. But as you can imagine, following the rules stated for child-parent, a bone can have more than one child but not more than one parent. That means that defined a bone in the skeleton, there is only one sequence of parents to reach the root parent of the skeleton. Also it means too that one root bone defines one skeleton so each skeleton has only one root bone and only one.
Consider this: B3 is child of B2 and B2 is child of B1. Also B4 is child of B2 and B5 is child of B4. The way to travel from B5 to B1 is unique: B5->B4->B2->B1.
Setup and Animation
During the animation of the skeleton it is supposed that the position of each bone, its angle and its scale changes. Position and angle are relative to the parent bone, but scale is a value that calculates the current length of the bone compared with the "original" bone length (scale=length'/length) as you can see from the original formulas in the previous section. That means that the "original" bone length shouldn't be never zero, otherwise there will be a division by zero and the scale of the bone becomes infinite.
Also, the final position P' of a point that moves influenced by a single bone is given by the original point position relative to the bone in its "original" position (P).
What I'm trying to explain is that it is needed that the setup of the bone (position, alpha and length) and the setup position of the point (P) to be moved would be given to calculate the final position of the point (P') given a moved position of the bone (position', alpha', length')
Said this and considered the information of the previous sections, the bones and points that are influenced from the bones should have the following parameters:
BONES PARAMETERS
| Parameter | Notation | Type | Animated | Comment |
|---|---|---|---|---|
| Origin | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle O_j(t) } | Vector (Real,Real) | Yes | Relative to the parent |
| Angle | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle \alpha_j(t) } | Angle (DEG) | Yes | Relative to the parent |
| Length | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle l_j(t) } | Real | Yes | Calculated, not animatable. |
| Scale | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle s_j(t) } | Real | Yes | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle l_j(t) =l^0_j \cdot s_j(t) } |
| Setup Origin | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle O^0_j(t) } | Vector (Real,Real) | Yes | Relative to the parent |
| Setup Angle | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle \alpha^0_j(t) } | Angle (DEG) | Yes | Relative to the parent |
| Setup Length | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle l^0_j } | Real | No | Constant, zero not allowed. |
| Setup Scale | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle s^0_j } | Real | No | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle s^0_j = 1 } |
| Parent | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle PBone_j(t) } | Bone | Yes |
POINT PARAMETERS
| Parameter | Notation | Type | Animated | Comment |
|---|---|---|---|---|
| Position | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle V(t) } | Vector (Real,Real) | Yes | Calculated: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle V(t) =VF(t) + VS(t) \cdot M(t) } Global coordinates |
| Free Position | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle VF(t) } | Vector (Real, Real) | Yes | Global Coordinates |
| Setup Position | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle VS(t) } | Vector (Real, Real) | Yes | Global Coordinates |
| Bone Influence Matrix | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle M(t) } | Matrix (3x3) | Yes | Calculated. See formulas below |
| Bone Influence Id | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle BoneID_i } | Bone | No | 'i' is the index for all the Bones that influences on the Point |
| Influence weight | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle w_i } | Real | Yes | the weight associated to the BoneID_i |
(t) denotes calculated at the time t
Position of a Point due to Bones Influence
According to the table, the final position of a point influenced by the bones is calculated based on two terms: A free movement of the point plus a bone drive movement. In this section we are going to calculate the second term.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle V(t) =VF(t) + VS(t) \cdot M(t) }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle M(t) = \cfrac{\sum_{i=1}^N M_i(t) \cdot w_i(t)}{\sum_{i=1}^N w_i(t)} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle M_i(t)=B^0_i(t) \cdot B_i(t) }
where i is a index that runs all the Bones Influence ID from i=1 to N (N= total number of bones that influence to the point)
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle B^0_i(t)= \prod_{j=root}^{j=i} C_j^0(t)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle B_i(t)= \prod_{j=i}^{j=root} C_j(t)}
where 'j' runs the bone skeleton jumping from a child/parent bone to a parent/child bone each time. The travel of the index 'j' from root to i and from i to root is fixed -and unique- by the nature of skeletons constructions (a bone, a parent), as mentioned before.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle C_j^0(t) = T(-O_j^0(t)) \cdot R(-\alpha_j^0(t)) \cdot S_x(\frac{1}{s^0_j})}
This matrix calculates the position of the point in local coordinates in relation to the bone 'j' at setup position. Notice that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle s^0_j } is equal to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle 1 } for any bone and for any time.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle C_j(t) = S_x(s_j(t))\cdot R(\alpha_j(t)) \cdot T(O_j(t)) }
This matrix calculates the global position of the point due to the bone 'j' at animated position of the skeleton.
Calculate the position and angle of a bone in a skeleton
Position and Angle at Setup
If the bones are described using relative coordinates to its predecessor, the position Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle Q^0_j} and the angle Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle \beta^0_j} of the bone 'j' in relation to the "master root bone" (ie. the global coordinate system) is given by those equations:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle Q^0_j(t) = O^0_j(t) \cdot B^0_j(t)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \beta^0_j(t) = \sum_{i=root}^{j} \alpha^0_i(t)}
where
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle B^0_j(t)=\prod_{i=root}^{parent} B^0_i(t)}
where 'i' goes form the root bone to the parent of the bone 'j' and climbs down by one child each time until it reaches the 'parent of bone j' bone of the skeleton.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle B^0_i(t)= T(-O^0_i(t)) \cdot R(-\alpha^0_i(t)) \cdot S_x(\frac{1}{s^0_j})}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle B^0_i(t)} is the inverse matrix transformation of the position of the bone relative to its immediate parent.
Notice that at setup, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle s^0_j} is always equal to 1.
Animated Position and Angle
Once calculated the position and angle of a bone in global coordinates you can calculate its animated position and angle by the transformation of their parents in the skeleton.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle Q_j(t) = O^0_j(t) \cdot B^0_j(t) \cdot B_j(t)}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \beta_j(t)= \beta^0_j(t) + \sum_{i=parent}^{root} \alpha_i(t)}
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle B_j(t)=\prod_{i=parent}^{root} B_i(t)}
where 'i' goes form the parent bone and jumps up by one parent each time until it reaches the 'root' bone of the bone 'j'.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle B_i(t)= S_x(s_j(t)) \cdot R(\alpha_i(t)) \cdot T(O_i(t)) }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle B_i(t)} is the transformation matrix of the position of the bone 'j' at the time t.
The results Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \textstyle Q_j(t), \beta_j(t)} are obtained in global coordinates.