Doc:Rescale Animations
Contents
Introduction
To rescale an animation means to modify the initial and final times when a portion of animation is shown. Imagine that you have created a complex animation for certain objects, but when you watch it with the rest of the backgrounds or other animated objects, it seems to be "out of time" (too late, too soon, too slow or too quick). You would like to modify the animation smoothly from one time segment [A-B] to other [C-D]. But how?...
You could think about moving the waypoints one by one and rescale the animation manually. Although it is possible, for the majority of the times it would be tedious and fruitless.
With Synfig it is easy to do.
Group the layers
First of all you need to group the layers that are going to be rescaled in time. We'll need to make use of the Time Offset Parameter of the Group layer.
Understanding what are we rescaling
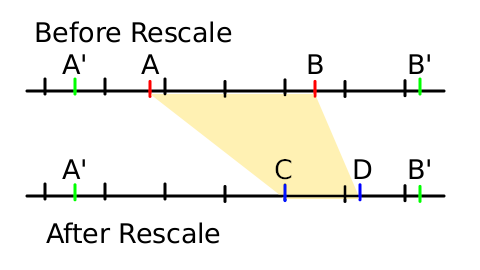
For example, say we want to rescale from [A-B] to [C-D]. So what we want is that when the original animation reaches the A time then the new animation would reach it at time C instead. Similarly for B and D. But if you move the animation in that way, what happens to the frames before frame A that are now before C? And what happens to frames after B that are now after D? Unless precautions are taken, they're rescaled too. Is that what we want? In the most general case we would like the frames 0f to A' (A'<A) and B' to the end of the animation (B'>B) to be untouched.
There are some conditions that the rescaled time segment [A-B], the desired time segment [C-D] and the untouched segments [0f-A'] and [B'- end] must fulfil:
- Frame A must be smaller than frame B. (Obviously)
- Frame C must be smaller than D.
- Frame A' must be smaller than A
- Frame B' must be greater than B
- Frames C and D must be smaller than B' and bigger than A'
(this diagram was done in Synfig :D)
Using the Group layer
Now we know what are rescaling, then let's modify the animation to make those changes on it.
Go to the Group layer you have obtained in the first step and go to its Time Offset Parameter. Insert the following waypoints in the animation of that parameter:
- At frame A', insert a value of 0f. This will maintain this frame untouched (and the ones that are before also, if there are no more waypoints there).
- At frame C, insert the result of subtracting from the time value at frame A, the time value at frame C (that is C-A in time units). It could be positive or negative. In the sample diagram it is negative and corresponds to -2s6f (if the animation is at 24fps and we assume that each division in the diagram is a second.)
- At frame D, insert the result of subtracting from the time value at frame B, the time value at frame D (that is D-B in time units). It could be positive or negative. In the sample diagram is negative and corresponds to -18f (if the animation is at 24 fps and we assume that each division in the diagram is a second.)
- At frame B', insert a value of 0f. This will maintain this frame untouched (and the ones that are after also, if there are no more waypoints there).
IMPORTANT: all the inserted waypoints must have linear interpolation. If not, you will change the original timing of the animation. To make it easy, just select Linear on the default interpolation parameter on the tool box window.
Examples
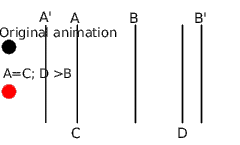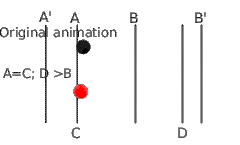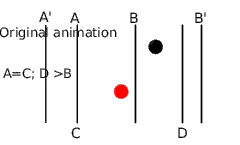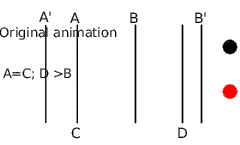
Enlarge a portion of animation at the end
In this case, the animation segment [A-B] is rescaled to [C-D] but A=C and D>B. You can see that in the original animation, the black circle has a constant velocity and the red rescaled one has the following motion:
- From A' to A, the animation is not touched (in fact A' can be the same as A because C is not smaller than A)
- From A=C to B, the rescaled animation is slowed down to reach B position at the same time the original animation reaches D. So the time segment [A-B] is rescaled to [C-D]. We've enlarged the time segment so the rescaled animation is slower.
- From B to B' the rescaled animation accelerates to reach the B' mark at the same time than the original. We've shortened the time from B to B' so the rescaled animation is quicker. It was done by setting the waypoint in the frame D to 0f, which forces the rescaled animation run to reach the original animation.
- From B' to the end, the animation is the same.
Both the original animation and the scaled animation use linear movement, but the scaled animation is done in three linear steps. In the original animation (black circle) the time and the position are the same. Hopefully this clarifies the example.
TO DO
Fix links to other wiki pages. Include an animation sample (in progress). Insert a table with the waypoints (time and value) of the offset parameter.